들어가기 앞서 . .
- 석사 과정 중에 공부하던 시계열 분석에 대해 기억을 더듬으며 정리할 예정이다. 시계열 분석이라는 항목이 수학적으로 정리하기 어렵고, 방법론도 다양해서, 글로 모든 내용을 정리하기 어려울 듯하다.
(시계열 분석 관련 작성했던 논문 --> 논문1(학위 논문) : [링크] , 논문2(국외 논문) : [링크])
- 이번에는 파이썬을 활용하여 가볍게 ARIMA모델을 적용해 비트코인 가격을 예측해보는 내용을 가볍게 다뤄보려 한다.
시계열 데이터 분석
- 시계열 데이터란 시간에 대해 순차적으로 관측되는 데이터의 집합을 말한다.
- 데이터 분석 혹은 모델링에서 독립변수(independent variable)를 이용해서 종속변수(dependent variable)을 예측하는 방법이 일반적이라면, 시계열 데이터 분석은 시간을 독립변수로 활용한다고 생각하면 된다.
- 현시점까지의 시계열 데이터를 활용해서 미래 시점의 데이터를 예측거나, 일정한 길이의 시계열 데이터를 이용해서 패턴을 분류한다거나 하는 등 분류나 예측을 통해 다양한 어플리케이션에 활용 할 수 있다.
- 전통적으로 시계열 데이터 분석은 AR(Autoregressive), MA(Moving average), ARMA(Autoregressive Moving average), ARIMA(Autoregressive Integrated Moving average) 모델 등을 활용해 불규칙적인 시계열 데이터에 규칙성을 부여하는 방식을 활용해왔다. 최근 딥러닝 방법이 발전함에 따라, 시계열 특성을 반영할 수 있는 RNN, LSTM과 같은 모델들을 시계열 예측에 활용하여 뛰어난 성능을 보여줬다.
- 하지만 시계열 데이터 분석을 잘 이해하기 위해서는 머신러닝 모델에 대한 이론보다는 통계적인 전통적 시계열 데이터 분석 방법을 잘 이해하는 것이 더욱 도움이 될 것이라 생각한다.
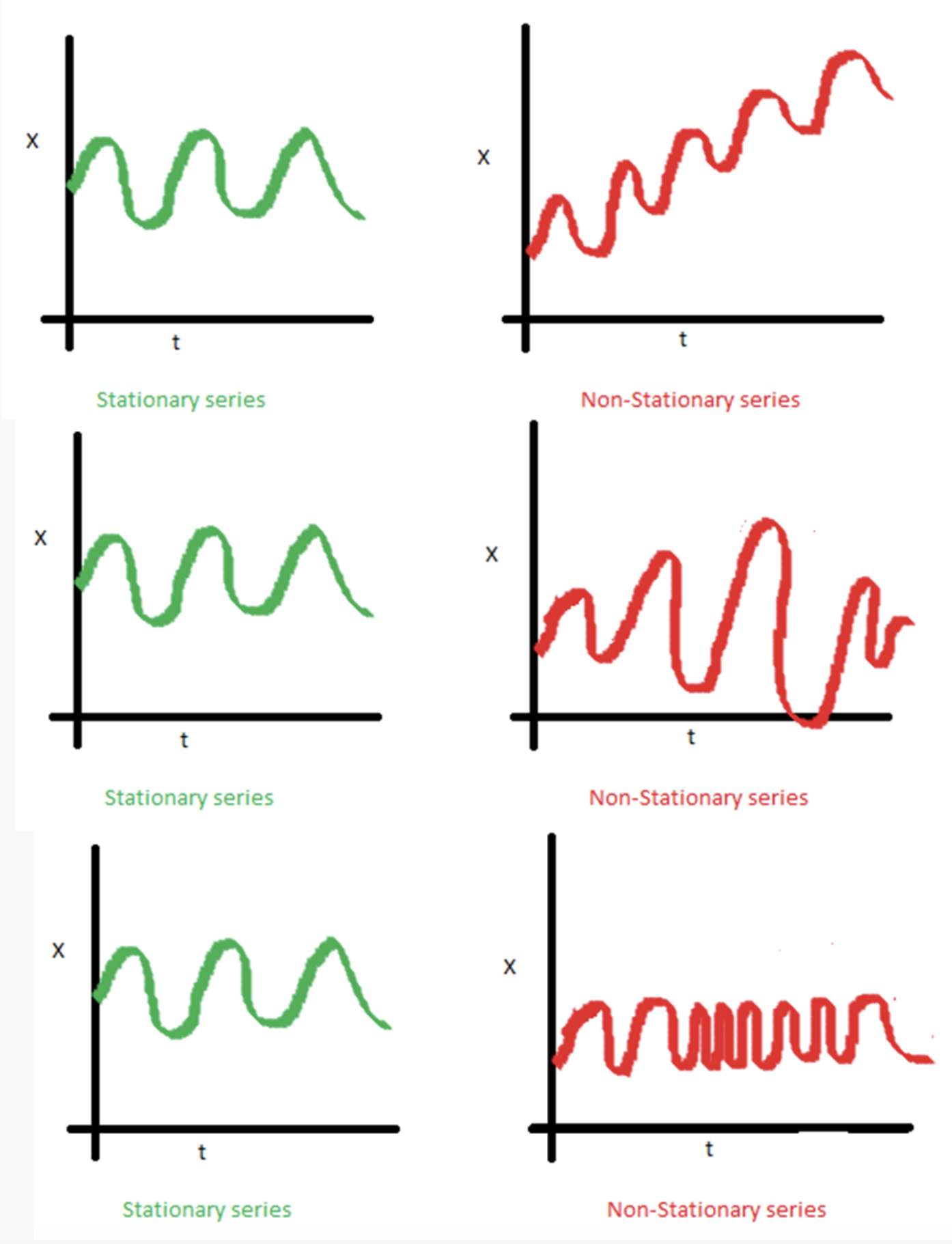
시계열 데이터의 정상성 (Stationary)
- 전통적으로 시계열 분석은 현재 시점까지 시계열 데이터의 확률적 특성이 시간이 지나도 그대로 유지 될 것을 가정하고 있다. 즉 시간과 관계 없이 평균과 분산이 불변해야하고, 두 개의 시점 간의 공분산이 다른 시점 과는 무관해야 한다.
1. Constant μ (mean) for all t.
2. Constant σ (variance) for all t.
3. The autocovariance function between Xt1 and Xt2 only depends on the interval t1 and t2.
Time series stationary condition
ARIMA Model
1) AR Model
Autoregressive 모델은 자기 회귀 모델이라고 불린다. 과거 시점의 자기 자신의 데이터가 현 시점의 자기 자신에게 영향을 미치는 모델이라는 뜻이다. AR(1)모델의 수식을 보면 아래와 같다. (AR의 차수 p=1 인 경우로 현재 시점부터 과거 p개 이전의 시점까지 데이터의 영향도를 보겠다는 뜻)
X(t) = w*X(t-1) + b + u*e(t)
위 수식을 보면 현재 시점 t에 대한 데이터는 이전 시점의 자기 데이터에 가중치 w를 곱하고 상수 b를 더하고(회귀식), error term인 e(t)에 가중치 u를 곱한 것을 더해서 표현할 수 있다. 여기서 e(t)는 white-noise라고 불리며, 일반적인 정규분포에서 도출된 random한 noise 값이다. 위에서 설명한 stationary와 관련된 것으로, 정상성 조건을 만족시키도록 하는 일종의 whitening이라고 하는 정규화로 보면 된다.
AR Model은 추세가 변하는 상황에서는 적합하지 않은 모델이다.
2) MA Model
Moving average 모델은 이동 평균 모델이라고 불리고, 트렌드 즉 추세가 변하는 상황에서 적합한 모델이다. MA(1) 모델을 수식으로 보면 아래와 같다. (MA의 차수 q=1인 경우로 과거 q개 이전의 변화율을 현재 시점에 반영하겠다는 뜻)
X(t) = w*e(t-1) + b +u*e(t)
위 수식을 보면 AR모델에서의 X(t-1)이 e(t-1)로 바뀌었다. 즉, 이전 상태의 자기자신을 보는 것이 아닌, 이전 항에서의 error텀을 현 시점에 반영하겠다는 뜻이다. 즉 변화율(추세)에 맞춰 추정하겠다는 의미다.
3) ARMA Model
ARMA는 1)의 AR과 2)의 MA모델을 합친 모델이다. 현재 시점의 상태를 파악하는 과거 시점의 자기 자신과 추세까지 전부 반영하겠다는 의미로, ARMA(1,1) 모델에 대한 수식을 보면 아래와 같이 간단하게 합칠 수 있다. (회귀 분석에서 독립 변수의 항이 늘어나는 개념)
$$ X(t) = w_{1,1}*X(t-1) + w_{2,1}*e(t-1) + b +u*e(t) $$
4) ARIMA Model
이제까지 AR, MA, ARMA모델의 경우 시계열이 정상성이라는 가정이 있는 상황에서 진행했다면, ARIMA모델에서는 차분이라는 개념을 통해 non-stationary한 상황에서 좀 더 나은 예측을 하는 것이 목표다. (현실세계의 데이터는 non-stationary한 경우가 대부분)
따라서 ARMA모델에 차분이라는 차수 d가 포함되어 ARIMA(p,d,q)로 표현할 수 있다.
차분이라는 개념은 현재 상태에서 바로 이전 상태를 빼주는 것을 의미하며, 차분을 거친 결과들이 whitening되는 효과를 가져온다.
차분을 수식으로 보면 아래와 같다.
$$ d = 0 : x_t = X_t $$
$$ d = 1 : x_t = X_{t} - X_{t-1} $$
$$ d = 2 : x_t = ( X_{t} - X_{t-1} ) - ( X{t-1} - X{t-2} ) $$
결국 1차분이 필요한 ARIMA(1,1,1)모델의 경우 ARMA(1,1)모델의 수식에서 X위치에 1차분이 들어간 식을 대입해주면 된다.
- (p, d, q) 차수의 결정
1) 차분 차수 d : 시계열 plot을 보고 정상성 여부를 확인하고, 차분을 진행하고, 차분 후의 plot을 보고 여부를 확인하는 프로세스로 진행한다.
2) p, q : p, q의 경우 보통 ACF(Autocorrelation function)와, PACF(Partial Autocorrelation function)를 보고 결정한다. ACF는 k lag 단위로 구분된 시계열 관측치 \(X_{t}\) 와 \(X_{t-k}\) 간의 상관 측도이고, PACF는 다른 모든 짧은 시차 항에 따라 조정한 후 k 시간 단위로 구분된 시계열의 관측치 \(X_{t}\) 와 \(X_{t-k}\) 간의 상관 측도 이다. (참고 : ACF. , PACF )
아래 표를 보면 ACF와 PACF plot의 형태에 따라 p와 q의 차수를 결정할 수 있다. (아래 예시를 통해 구체적으로 확인)
| ACF | PACF | |
| AR(p) | ACF plot이 서서히 감소하는 형태 | PACF plot이 p lag 이후 절단되는 형태 |
| MA(q) | ACF plot이 q lag 이후 절단되는 형태 | PACF plot이 서서히 감소하는 형태 |
비트코인 예측 (2020년 4시간 간격의 데이터 기준)
(관련 소스는 Github [링크] 참고)
1) 데이터
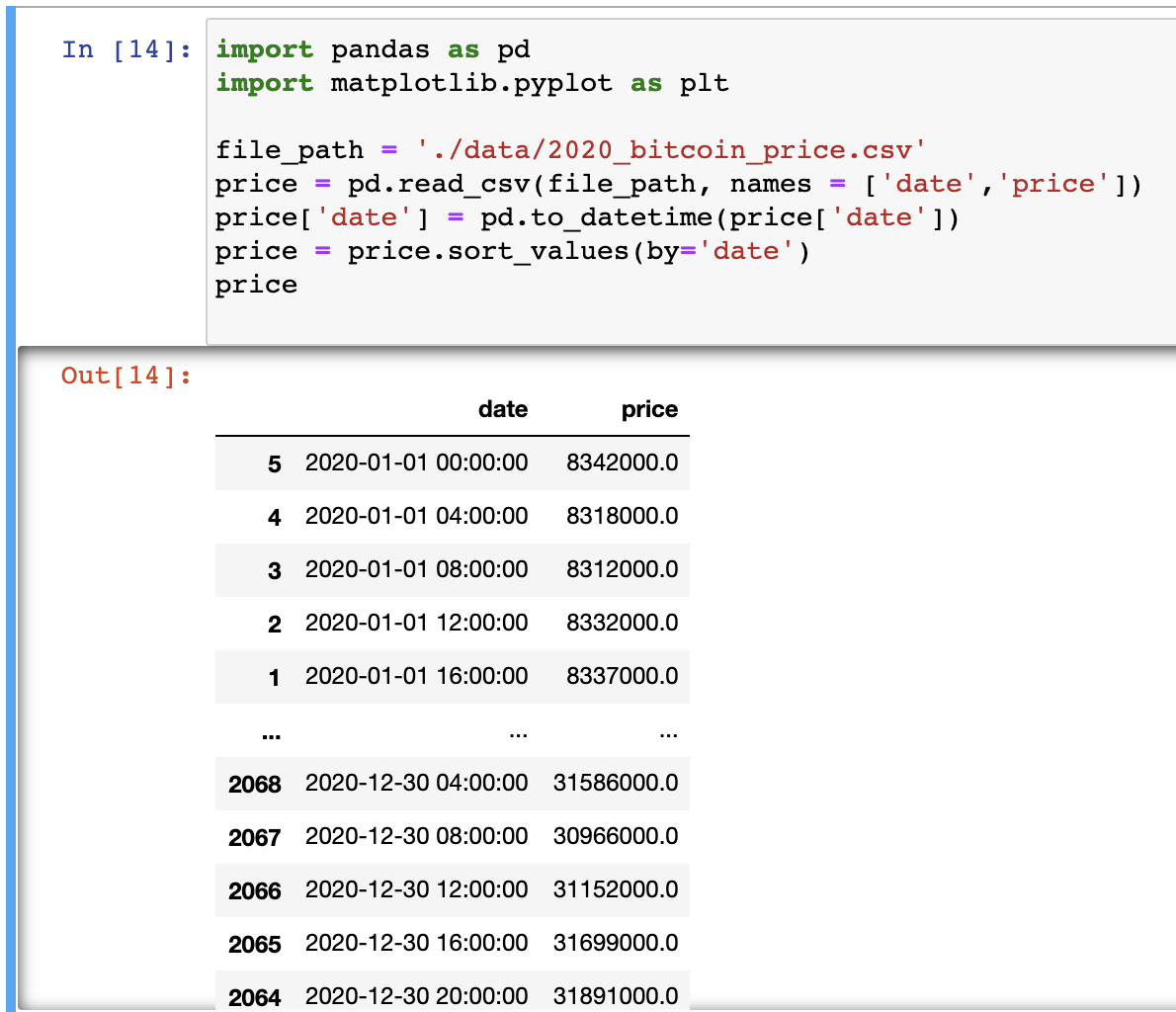
데이터는 위의 이미지와 같이 4시간 단위로 정렬된 비트코인 가격에 대한 1년치 데이터이다.

맨 끝의 4개 데이터를 테스트 데이터로 하고, 나머지 데이터로 ARIMA모델을 만드려고 한다. 위의 이미지로 비트코인 가격에 대한 plot을 그려보면 stationary한 시계열이 아니기 때문에 차분이 필요하다는 것을 알 수 있다.
2) 차분
아래 이미지와 같이 가격에 대해 1차, 2차 차분을 한 모습이다.
1차 차분의 경우 일부 지점에서 평균이 일정하지 못한 것을 확인할 수 있었다. 따라서 2차 차분이 적절해 보이므로 d=2로 정했다.

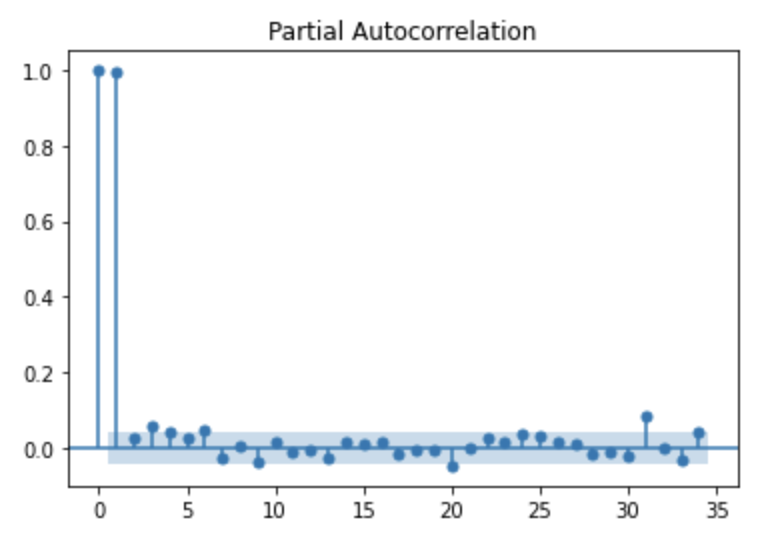
3) ACF , PACF
비트코인 가격으로 ACF, PACF plot을 그려보면 아래와 같다. ACF는 점진적으로 감소하고, PACF의 경우 자기자신을 제외한 첫번째 lag 이후 절단면을 보이므로 AR 오더는 1, MA 오더는 0이 적절하다는 것을 알 수 있다.

4) ARIMA(1,2,0) Model summary
ARIMA(1,2,0) 모델에 대해 각 변수에 대한 p-value를 보면 상수항의 p-value가 높아 유의미하지 않다는 것을 알 수 있었다. 따라서 모델을 fitting할 때 trend = 'nc'로 해두는 것이 적절했다.

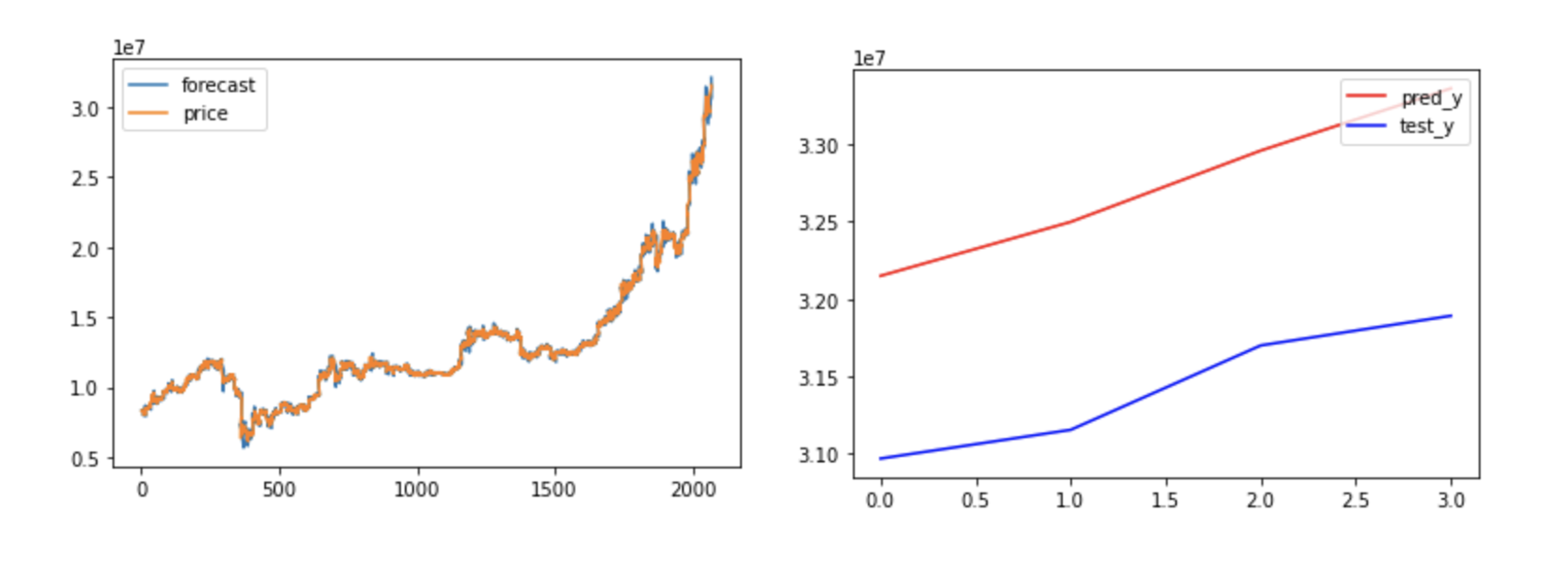
5) 결과
아래 결과 plot이미지를 보면, 먼저 모델이 학습데이터에 대해서 잘 fitting된 것을 확인할 수 있었다. 그리고 4시점에 대한 데이터 예측 결과는 추세는 잘따라가는 편이었지만, 오차는 어느정도 있었다.
보통 시계열 데이터 예측의 오차 지표로 사용하는 RMSE값을 보더라도 꽤 높은 것을 확인할 수 있었다.
마무리
- 전통적인 시계열 예측 방법인 ARIMA에 대해 아주 심플하게 정리해봤다. ARIMA같은 경우는 종속 변수만을 가지고 예측을 하기 때문에 다양한 feature들을 활용하기 어렵다. 이후에 다변량 시계열 데이터를 다루는 다양한 방법들(ARIMAX, VAR, VARMA등)을 정리해 봐야겠다.